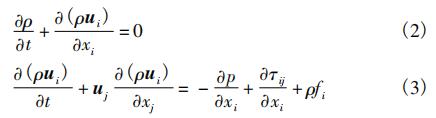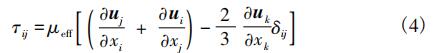供稿作者:劉春哲1,張濤2,田輝1,曼茂立1,3,趙海賢1,孫占剛1,楊博4,豆廣東5
供稿單位:(1.承德石油高等專科學校機械工程系,河北承德067000;2.河北機電職業(yè)技術學院,河北邢臺054000;3.河北省儀器儀表產業(yè)技術研究院,河北承德067000;4.承德石油高等專科學校科技發(fā)展與校企合作處,河北承德067000;5.承德石油高等專科學校招生就業(yè)處,河北承德067000)
摘要:為了揭示旋渦進動效應所產生的渦旋低壓流場演化規(guī)律,從而為旋進旋渦流量計壓力傳感器選型及安裝位置提供依據(jù),對DN50某型號
旋進旋渦流量計內全三維非定常流場進行數(shù)值分析。經過實驗驗證,所采用的定常-非定常兩步走的數(shù)值求解策略能準確獲得低壓區(qū)壓力脈動頻率特性,所得儀表系數(shù)與實驗值吻合良好。數(shù)值模擬結果完整呈現(xiàn)了旋渦進動效應影響下沿軸向及周向壓力脈動規(guī)律。為了保證和擴大量程比,給出壓力傳感器低壓區(qū)的靈敏度、傳感器尺寸及位置的選擇依據(jù)。
關鍵詞:旋渦進動;數(shù)值模擬;壓力脈動;非定常;壓力傳感器
前言
隨著20世紀七十年代DIJSTELBERGEN[1]對旋進旋渦流量計原理的開創(chuàng)性研究和闡述,美國時代公司旋進旋渦流量計產品一經推出便因其無運動部件、可靠性強、適應測試工質范圍廣等優(yōu)勢受到相關用戶和學者的關注[2-3]。然而,相對于其他
流量計,至今旋進旋渦流量計測試原理尚不完善。HEINRICHS[4]就旋進旋渦流量計信號處理、儀表性能及標校進行了論述。21世紀初,傅新等人[5]在國內非常早對旋進旋渦流量計進行系統(tǒng)研究,應用計算流體力學理論解釋了旋渦產生和發(fā)展的基本原理并對測試環(huán)境存在震動干擾的情況下如何實現(xiàn)信號采集和處理以保證測量精度做了深入的研究。然而,限于當時的研究條件,旋進旋渦的進動效應數(shù)值研究結果與實驗值存在較大的偏差,數(shù)值研究結果對解決實際問題指導不足[6]。此后,彭杰綱等[7]、崔寶玲等[8]、張濤等人[9]、吳蕾[10]的研究均對旋渦進動頻率與流量的相關理論作了一定的補充。在此基礎上,本文作者對 DN50 某型號旋進旋渦流量計旋渦進動流動特性進行了詳細的數(shù)值研究,給出了不同流量下旋進旋渦的進動周期和頻率特性,完整呈現(xiàn)了旋渦進動效應影響下流場的壓力分布情況,特別是針對測試段特征點上的壓力脈動情況為壓力傳感器靈敏度及位置選擇提供依據(jù)。
1 旋進旋渦流量計測量原理簡介
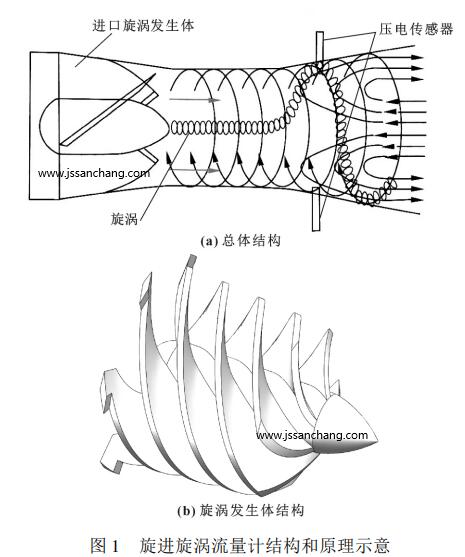
旋進旋渦流量計主要由旋渦發(fā)生體、漸縮管、漸擴管、壓力傳感器組成[11]。如圖 1 所示,旋渦發(fā)生體通常由若干個螺旋線形葉片組成,被測來流經過葉片間組成的旋轉流道后形成沿軸向的旋渦流; 旋渦流在旋渦發(fā)生體尾部發(fā)生分離,從而形成具有顯著低壓特性的 “渦核”; 渦核隨主流流經漸縮管形的流道,軸向速度不斷提升; 此后進入漸擴形的流道,伴隨流道通流面積的增加引起流道中部區(qū)域發(fā)生回流現(xiàn)象,渦核在此回流的作用下被推離流道中心位置并與主流一起形成旋渦流。DIJSTELBERGEN[1] 發(fā)現(xiàn)在流道漸擴段,渦核沿周向的周期性進動運動與主流的體積流量成正比,所以可通過壓力傳感器測得渦核進動頻率f 來推算體積流量 Q,進而實現(xiàn)對流量的測量。
Q = f /K ( 1)
式中: K 為儀表系數(shù),表示流過單位體積的工質時渦核周向旋轉運動所引起的壓力脈動次數(shù); Q 為被測氣體流量,m3 /h; f 為壓力脈動頻率,Hz。
本文作者所研究的旋進旋渦流量計全長 162 mm,喉部直徑 16 mm; 旋渦發(fā)生體由 6 個螺旋線形葉片組成,固定螺距為 60 mm,葉片沿軸向長 48 mm。為了提高模型計算收斂性,分別對旋進旋渦流量計物理模型前段及后端延長 1D ( D 表示公稱直徑,文中所選流量計為 DN50 型) 。所有近壁面區(qū)域設置 5 層邊界層網格,并采用連續(xù)過渡方式與內部區(qū)域網格進行銜接。狹縫區(qū)域網格不小于 5 個,旋渦發(fā)生段及入口延伸段采用四面體網格,其余部分采用六面體網格。經過網格無關性驗證,非常終采用網格約為 225 萬,如圖2 所示。
2 數(shù)值模擬方法
對于旋進旋渦流量計內的全三維黏性非定常流動可用 Navier - Stokes 方程組[12]描述,其連續(xù)性方程及動量方程表示為
式中: ρ 為工質密度,kg /m3 ; ui 為速度矢量,m/s; p 為靜壓,Pa; fi 為質量力,文中僅指重力,N; 應力張量 τij可表示為
等效黏性系數(shù) μeff可通過工質動力黏性系數(shù) μ 與湍流黏性系數(shù) μt 之和獲得,湍流黏性系數(shù)可通過引入湍流模型獲得。
計算過程分兩步進行: 首先給定入口質量流量,出口給定靜壓,所有壁面給定無滑移邊界條件,流場特征參數(shù)穩(wěn)定且殘差均小于 10 - 3時,認為定常計算已收斂,接著進行非定常計算; 非定常計算階段,以當前流場入口總壓作為非定常計算的入口邊界條件,時間步長在非定常計算過程中不斷調整以使其在壓力脈動周期的 1 /20 ~ 1 /30 范圍內。Navier - Stokes 方程組采用具有二階精度的有限差分方式離散,SIMPLE 算法解耦速度場及壓力場,引入重整化群 κ - ε 湍流模型。 3 計算結果及分析
3. 1 旋渦進動過程的捕捉
如圖 3 ( a) 所示,為某校與某公司共同開發(fā)的音速噴管氣體流量計標定實驗臺,此裝置可對包括DN50 在內 6 種口徑、0. 5 ~ 256 m3 /h 流量范圍的
氣體流量計進行標定,其中橢圓區(qū)域為流量計安裝位置。
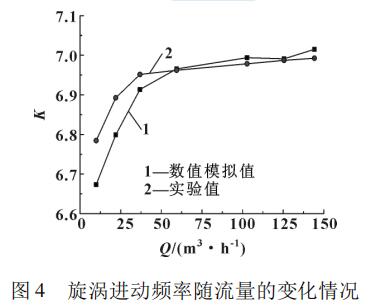
基于此實驗系統(tǒng),對圖 3 ( b) 所示的旋進旋渦流量計進行測試,圖中喉部測量段顯示了測壓孔的位置并標記出了測壓面的位置。圖 4 給出了不同流量下旋進旋渦流量計儀表系數(shù)實驗值與數(shù)值模擬結果的變化情況。可以看出: 數(shù)值模擬結果與實驗值趨勢吻合良好,二者的非常大偏差約為 3. 6% 。由此可以驗證文中數(shù)值模擬方案的準確性和有效性。
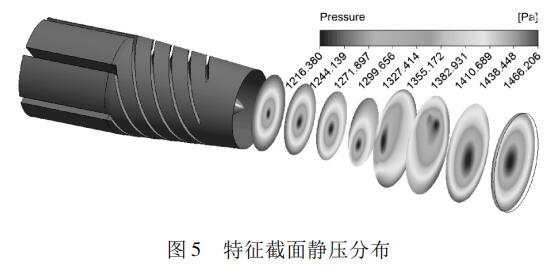
如圖 5 所示,給出了流量為 60 m3 /h ( 滿量程的40% ) 時,沿著旋進旋渦流量計主流方向,8 個特征截面靜壓分布情況。可見: 被測氣體流過起旋器后( 圖中左側部分為入口延伸段及起旋器) ,在起旋器尾部中央發(fā)生了流動分離,產生旋渦,形成了圓形低壓區(qū),截面靜壓沿半徑方向不斷增加。被測氣體沿漸縮管向下游流動過程,低壓區(qū)核心部分面積基本保持穩(wěn)定,并始終處于流道中心。當被測氣體進入漸擴段時,發(fā)現(xiàn)低壓區(qū)核心位置偏離了流道中心區(qū)域,這是由于漸擴段流道中央存在回流,擠壓迫使低壓旋渦發(fā)生偏離造成的。此后,旋渦偏離流道中心旋轉,使得低壓區(qū)核心部分被拉伸,呈 “彗星” 狀。接近出口處,低壓區(qū)有向流道中心靠攏的趨勢。
3. 2 旋渦進動對壓力分布的影響
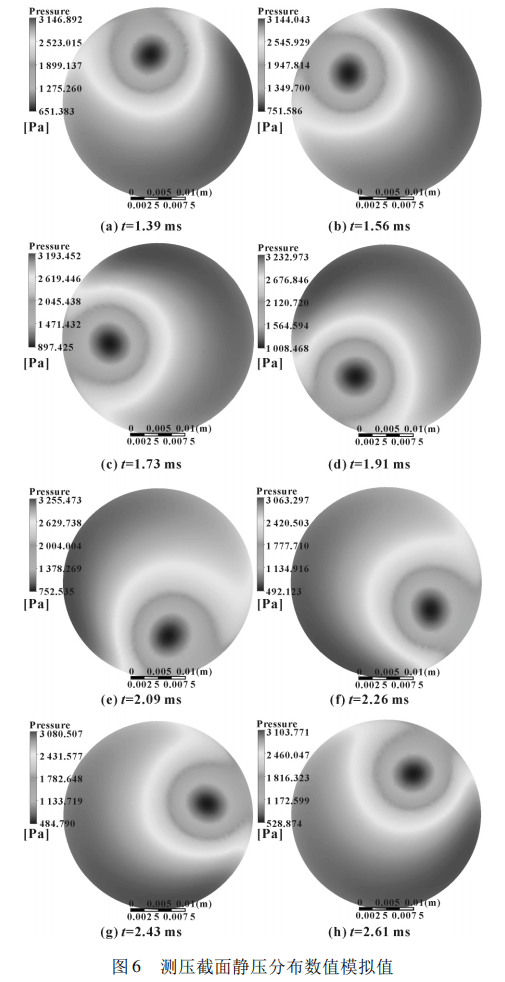
圖 6 中給出了流量為 100 m3 /h ( 滿量程的 67% )時 8 個時刻測壓截面的靜壓分布數(shù)值模擬值,暖色區(qū)域為高壓區(qū),冷色區(qū)域為低壓區(qū)。可見: 旋渦核心區(qū)所形成的藍色低壓區(qū)沿著逆時針方向做圓周運動,且低壓核心位置距離流道中心的距離保持不變。圖 5 及 圖 6 的數(shù)值計算結果完整展示了旋渦的進動運動,其流動規(guī)律符合彭杰綱[7]的研究成果。文中數(shù)值模擬所得該工 況 旋 渦 進 動 頻 率 約 為 699. 8 Hz,與 實 驗 值718. 1 Hz 十分接近,從而克服了文獻 [7] 中脈動頻率預測失真的問題。
旋進旋渦流量計進行流量測量的關鍵是通過傳感器準確獲得測壓截面內壓力脈動情況,進而對壓力信號進行處理獲得脈動頻率,計算出實際流量[1,5]。如 圖 7 所示,給出了 4 個工況測壓點處壓力隨時間變化的數(shù)值模擬結果。測壓點為位于圖 3 ( b) 所示的測壓截面上,距離軸心 8 mm 處。從圖 7 可見: 不同工況下測壓點處壓力均呈現(xiàn)出較強的周期性脈動特點,且隨著實際流量的增加脈動周期顯著降低,脈動幅值顯著增加。小流量 10 m3 /h 下,壓力脈動周期約為15. 2 ms,壓力脈動在 10 ~ 33 Pa 內; 大流量 150 m3 /h 下,壓力脈動周期約為 0. 98 ms,壓力脈動則增加至1 900 ~ 7 000 Pa 內。由此可見,為了實現(xiàn)全量程的高精度,流量計所采用的
壓力傳感器需具備探測小流量下微壓差的能力。
此外,圖 7 中壓力脈動曲線顯示,每個脈動周期中低壓區(qū)所占時間隨流量的增加不斷降低,這說明每個工況下低壓區(qū)面積隨流量的增加是逐漸降低的。若將某一工況第 i 個周期的非常大壓力及非常小壓力記為: pimax、pimin,則壓力脈動的中值可近似表示為 ( 文中求解不少于 5 個周期的脈動情況,即 n > 5) :
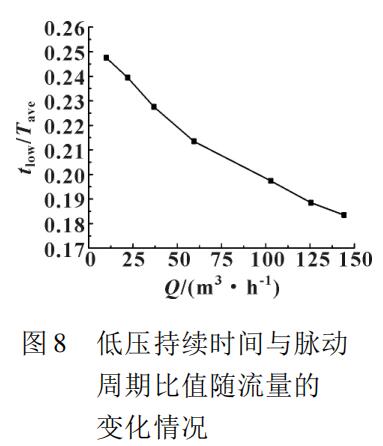
若將某一工況第 i 個周期中測壓點壓力值小于壓力脈動中值的時間記為tlow,則 tlow 與壓力脈動平均周期 Tave的比可以定量反映旋進旋渦進動過程在測壓面上形成的低壓區(qū)面積。圖 8 中可見: 隨著流量的增加,tlow /Tave不斷降低,當流量超過100 m3 /h的時候,tlow /Tave已小于 0. 199。也就是說,當流量達到 100 m3 /h 時,一個直徑為 5 mm 的壓力傳感器,在測壓面上徑向距軸心 8 mm 處,由于低壓區(qū)面積較小( 達不到直徑 5 mm 的圓形區(qū)域大小) ,造成壓力傳感器時刻承受高壓或高低壓共同作用,進而無法準確地對低壓進行探測,導致大流量時壓力脈動信號減弱的問題。由此可見,為了保證大流量下壓力脈動的探測精度,壓力傳感器直徑與其所在位置圓周長之比,應小于滿量程時 tlow /Tave的值。以上結論可為旋進旋渦流量計壓力傳感器的安裝位置及尺寸選擇提供依據(jù)。
4 結論
( 1) 基于在時間/空間上均具備二階精度的非定常湍流數(shù)值計算方法,對旋進旋渦流量計旋渦進動流動特性進行了詳細的數(shù)值研究。數(shù)值計算所得測壓點壓力脈動頻率特性與實驗值吻合良好,驗證了文中數(shù)值方法的有效性。
( 2) 數(shù)值結果完整呈現(xiàn)了旋渦進動效應影響下,沿著軸向旋渦所引起的低壓區(qū)分布規(guī)律,以及測壓截面上隨著時間的推移低壓區(qū)的遷移規(guī)律。
( 3) 隨著流量的增加,脈動幅值及壓力值從小流量的幾十帕斯卡增至滿量程的數(shù)千帕斯卡,這就要求所采用的壓力傳感器需具備較寬的測量范圍,且在小壓力范圍內具有較高的靈敏度; 隨著流量的增加,旋進旋渦所形成的低壓區(qū)沿著周向所占據(jù)的面積不斷降低,為了保證壓力傳感器能探測到低壓區(qū)的存在,壓力傳感器直徑與其所在位置圓周長之比應小于滿量程時 tlow /Tave的值。